La ecuación más bella

En este 2007 se cumplen 300 años del nacimiento de Leonhard Euler, uno de los matemáticos más productivos y geniales de todos los tiempos. En honor a él, esta entrada en el blog con la considerada por muchos de forma unánime como la ecuación más bella de las matemáticas.

La ecuación involucra de forma fascinante a los cinco números más emblemáticos de las matemáticas, 0, 1, i (unidad imaginara igual a raíz cuadrada de -1), y los números irracionales pi (3,141592…) y e (2,718281…, base de los logaritmos neperianos).

Matemáticas y Cine II

Una Mente Maravillosa
Una mente maravillosa es un película fantástica, fue la película triunfadora en los Oscars del año 2002, con 4 estatuillas, entre ellas, la de mejor película. La película está basada en la biografía (escrita por Sylvia Nasar)del matemático John F. Nash . En el film, dirigido por Ron Howard, se introduce al espectador en el difícil mundo de la investigación matemática, del esfuerzo y la dedicación que supone conseguir las metas que uno se propone, y sobre todo de lo necesario que es el apoyo de las personas que te quieren.
La teoría de juegos, objeto de la investigación de Nash, estudia las estrategias óptimas así como el comportamiento previsto y observado de individuos en los juegos, teniendo numerosas aplicaciones en economía, filosofía y biología. Nash consiguiría el nobel por la teoría del equilibrio en los juegos en 1994. Hoy en día J.F. Nash es una leyenda viviente que sigue entregado a su trabajo.

Sipnosis
La película es una historia de amor que tiene a las matemáticas como telón de fondo, un drama intensamente humano sobre John F. Nash. Éste, un genio de las matemáticas, ve atacada su brillante mente por la esquizofrenia. Cualquier otra persona hubiera abandonado con esta enfermedad, pero Nash luchará por recuperarse con la ayuda de su esposa Alicia, y tras varias décadas de sufrimiento logrará superar su tragedia.

Reparto
Russell Crowe, Ed Harris, Jennifer Connelly y Christopher Plummer

Año
2001

Nota para intrépidos/as: En la película aparece que el irracional pi está entre 0 y 1, cosa que es absolutamente falsa. (ver en el cristal de la foto de arriba justo en la cara de Russel Crowe)

Los Logaritmos.

Hablar de Logaritmos en los institutos es hablar de sufrimiento para los alumnos, porque esta herramienta matemática se les atraganta hasta tal punto de tenerle miedo nada más nombrarlos. ¿Por qué aparecieron y cuándo? son dos buenas preguntas que vamos a intentar responder para hacer los logaritmos más accesibles.
Los principios del Siglo XV vivieron una extraordinaria expansión del tráfico marítimo, esto a su vez provocó la necesidad de disponer de más cartas astronómicas (mapas de del mar) y más precisas para orientarse en alta mar. Estas cartas requerían una gran cantidad de cálculos, y algunos de ellos bastante complejos (multiplicaciones y divisiones de números de muchas cifras). Como en ese tiempo no existía la calculadora, los matemáticos inventaron una herramienta que viniera ayudar en esta labor. ¿Adivinan cuál? Si, como pensaban fueron los logaritmos. La solución parte de la idea de transforman productos en sumas y divisiones en restas, porque evidentemente las sumas y las restas son más fáciles de calcular que las multiplicaciones y divisiones.

Así los logaritmos permitieron que astrónomos y científicos continuasen con su trabajo desembarazándolos de tediosos cálculos.

Veamos cómo funcionaban con un ejemplo. Supongamos la tabla de las potencias de 2:

1	2	3	4	5	6	7	8	9	10
2	4	8	16	32	64	128	256	512	1024

Si queremos hacer 16 · 64 equivale a 4 + 6 = 10, lo que significa que el producto va a ser el número situado encima del 10, esto es,1024. Y si queremos dividir 512 entre 32 hacemos 9 – 5 = 4, lo que nos dice que el resultado es 16.
Así de forma natural aparece la definición de logaritmo de un número en cierta base, como una generalización de la tabla anterior: Loga b = c (se lee logaritmo en base a del número b)porque "a" elevado a "c" = b

Por ejemplo, Log 2 32 = 5 porque 2 elevado a 5 son 32, y Log2 128 = 7 porque 2 elevado a 7 son 128. Fue John Napier (1550-1617) en 1614 el que dio esta definición, si bien Michael Stifel ya había estudiado esta relación entre las potencias de un número y sus exponentes. No obstante se cree que Joost Bürgi (1552-1632) los descubrió seis años antes pero por motivos que se desconocen no lo publicó.

En 1617, aparecían las primeras tablas logarítmicas de números entre 1 y 1000 (generalización de la tabla anterior) con 14 decimales, y posteriormente de más y más números. Estas tablas serían muy útiles hasta que llegaron las calculadoras y las teclas Log y Ln, que nos dan el logaritmo de cualquier número en base 10 y base “e=2.71…”. Ln se llama logaritmo neperiano y debe su nombre a Napier.

Aplicaciones de los Logaritmos.

La escala de Richter es un ejemplo de Escala Logarítmica

Dentro del campo de las ciencias, los logaritmos son una herramienta fundamental a la hora de resolver ecuaciones, de analizar ciertos fenómenos mediante la función logarítmica (función recíproca de la función exponencial), y muchas cosas más.Pero dejando lo estrictamente matemático, una de las mayores aplicaciones de los logaritmos son las escalas logarítmicas.

¿Qué son y para qué se utilizan las escalas logarítmicas?
En la Naturaleza se dan situaciones en que se tienen que utilizar medidas de órdenes muy diferentes. Por ejemplo, Los pesos de los seres vivos:
un hombre puede pesar 90 kg = 90.000 gr = 10 elevado a 4,96 gr
un rotífero (el menor animal pluricelular): 0,00000000603 gr = 10 elevado a –8,22 gr
una ballena (el mayor de todos los animales): 120 Tm = 120.000.000 gr = 10 elevado 8,08 gr

Así que si tenemos que referirnos a diferentes animales por sus pesos o hacer una gráfica con los mismos, es un gran inconveniente que haya tan enormes diferencias entre unos y otros. Una solución para abreviar la expresión de esas diferencias es asignar a cada animal el logaritmo decimal de su peso, al que llamaremos el “orden de magnitud”. Por ejemplo: El rotífero:-8'22, la mosca:-5'30 , el escarabajo gigante (mayor insecto): 2'00, el hombre: 4'96, el avestruz: 5'20, el cocodrilo: 6'25, el elefante: 6'99, la ballena: 8'08
Ahora ya podemos, por ejemplo, hacer una escala con todos los animales que no sea excesiva. El orden de cada animal será un número entre –8 y 8 y llamaremos:

• muy pequeños, a los animales de órdenes entre -8 y –5
• pequeños, entre –5 y –2
• medianos, entre –2 y 2
• grandes, entre 2 y 5
• muy grandes, entre 5 y 8.

Esto es lo que se llama una escala logarítmica. En un rango pequeño, en este caso de -8 a 8, que consigue expresar realidades muy diferentes.
Ejemplos famosos de escalas logarítmicas son:

1. La escala para la medición de la intensidad del sonido.
   La presión del sonido que llega hasta nuestros oídos se mide en pascales. El intervalo de sonidos que puede percibir el ser humano oscila entre 0’00002 y los 100 pascales (umbral del dolor), es un intervalo tan amplio que resulta inmanejable, por lo que se adopta un escala logarítmica expresada en decibelios desde 0 a 180 db.
2. El Ph.
   Que es una medida de la acidez de una concetración (número de iones H3O+).
3. La escala Richter.
   Mide la intensidad de los terremotos que que es una magnitud que oscila entre 3’5 (casi impercertible) y 8 (Gran terremoto)
4. La magnitud aparente.
   La magnitud aparente de una estrella, planeta o de otro cuerpo celeste es una medida de su brillo aparente, es decir, la cantidad de luz que se recibe del objeto (el brillo aparente no es igual al brillo real, porque un objeto muy brillante puede estar muy muy lejos). Así por ejemplo, en esta escala al sol le corresponde una magnitud aparente de –26’8, a la luna –12’6, y a las estrellas más débiles visibles por el ojo humano +6.

Para más información: http://es.geocities.com/mundo_matematicas/

Chistes Matemáticos

Para que nos riamos un rato, algunos chistecitos de mates:

• En la fiesta de los ceros.
  Esta era una fiesta de ceros...
  Llega el 10, y lo paran en la puerta. El 10 les dice : "Oye, ¿acaso no puedo andar con bastón?".
  Llega el 101, y cuando lo paran dice: "Oye, ¿no ves que ando con muletas?".
  Llega el 7, y cuando lo paran dice: "Bah, es que pensé que era una fiesta de disfraces".
  Llega el infinito, y le dicen: "Ah, no, usted no entra". Y el infinito dice: "Desgraciado, nos discriminas por ser siameses".
  Llega el 1 y le dicen: "¿Y usted?".Responde: "Es que me puse a dieta".
  Llega el 8, y le dicen: "Usted sí que no entra, y no me diga que viene disfrazado". Y el 8 dice: "No, yo soy un 0, pero vine con cinturón".
  Llega el 6 y antes de que lo paren dice: "¿Qué pasa?. ¿No te gustan los Punk?".
  Llega el 40 y dice: "Yo pensé que podía traer a mi novia".
  Llega el 9 y le dicen: "Señor, si quiere entrar, ¡súbase la bragueta!".
• ¿Cuánto son 2+2 para un ...?
  Ingeniero: 3.9999989, Físico: 4.0004 +/- 0.0006, Matemático: espere sólo unos minutos mas, ya he probado que la solución existe y es única, ahora la estoy acotando, Filósofo: ¿Que quiere decir cuando dice "2+2"?, Informático: defina las características de la operación "+" y le responderé, Contable: cierra puertas y ventanas y pregunta en voz baja "¿cuánto quiere que sea el resultado?".
• Oveja Negra.
  Un físico, un ingeniero y un matemático van en un tren por Gales,y al observar por la ventana ven una oveja negra.- Ahh, dice el físico, "veo que las ovejas galesas son negras".- Mmm..., dice el ingeniero, "querrás decir que algunas ovejas galesas son negras".- No, dice el matemático, "todo lo que sabemos es que existe al menos una oveja en Gales, y que por lo menos uno de sus lados es negro".
• Pregunta en clase.
  El maestro.- "A ver, Jaimito, contesta rápidamente: ¿Cuántos son dos y dos?".
  Jaimito.- "Cinco".
  El maestro.- "¿Cómo puedes ser tan burro?".
  Jaimito.- "Pero usted qué quiere, ¿rapidez o precisión?".
• Examen de límites.
  En Bilbao, al salir de un examen de Análisis Matemático:
  - "Oye Patxi, ¿qué te ha dado el segundo límite, pues?".
  - "Más infinito".
  - "¿Sólo?".
• Aritmética de la pareja.
  Hombre inteligente + Mujer inteligente = ROMANCE
  Hombre inteligente + Mujer tonta = AVENTURA
  Hombre tonto + Mujer inteligente = MATRIMONIO
  Hombre tonto + Mujer tonta = EMBARAZO
• Aritmética de la empresa.
  Jefe inteligente + Empleado inteligente = BENEFICIO
  Jefe inteligente + Empleado tonto = PRODUCCIÓN
  Jefe tonto + Empleado inteligente = ASCENSO
  Jefe tonto + Empleado tonto = HORAS EXTRA

Pi y el fomento de la memoria

Este famoso número como todos sabemos es irracional, lo que significa que es un número con infinitas cifras decimales que no se repiten nunca. Este hecho ha fomentado en muchas personas la afición de memorizar sus cifras.
Uno de los casos más llamativos ha sido el del japonés Hideaki Tomoyori de cincuenta y cuatro años, natural de Yokahama, que fue capaz de recitar las 40.000 primeras cifras de pi de memoria en diecisiete horas y veintiún minutos, insertando pausas por un total de cuatro horas y quince minutos. Esta hazaña tuvo lugar los días 9 y 10 de mayo de 1987.

El truco para memorizar todos estos números es utilizar reglas nemotécnicas, que ayuden a recordar todos las cifras decimales. Algunas personas por ejemplo se crean historias usando palabras con un número de letras igual a la cifra décimal.

Para terminar las 200 primeras cifras decimales del número Pi.
Pi = 3’14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32832 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196…

Fuente: La sonrisa de Pitágoras

Ramanujan

Cualquier número entero positivo era un amigo personal suyo. (Con esta frase Littlewood hablaba de su colega Ramanujan)

Ramanujan (foto de pasaporte)

La historia de Ramanujan es una historia triste, pero que a su vez merece la pena ser contada, porque la vida está llena de estas personas y el mejor tributo para ellas es que con el paso de los años no caigan en el olvido. Con Ramanujan siempre se te queda la pregunta de qué hubiera pasado si hubiera nacido en otro lugar.

Srinivasa Ramanujan (1887-1920) tuvo una infancia difícil porque sus padres eran bastante pobres. Fue lento en aprender a hablar, pero pronto destacó en la escuela por sus dotes para las matemáticas "Se divertía repitiendo los valores de pi y de la raíz cuadrada de dos con cualquier número de cifras decimales a sus amigos". Después de terminar sus estudios básicos Ramanujan tenía claro que quería dedicarse a las matemáticas, pero desgraciadamente en esa época en la India no había lugar para profesionales de esta ciencia y aunque consiguió algunas becas terminó por buscar trabajo en las oficinas de la Compañía del Puerto de Madrás. ¡Qué paradoja! Uno de los genios matemáticos más grandes de la historia (como lo calificaría Hardy) debe abandonar en parte su carrera profesional para conseguir dinero para comer.

Pero para él las matemáticas eran su pasión y lejos de desanimarse de forma autodidacta y con mucho esfuerzo, llegó a completar unos cuadernos que contenían entre 3000 y 4000 teoremas, de los cuales casi dos tercios de ellos eran nuevos en matemáticas y el resto descubrimientos independientes de los ya realizados por otros matemáticos. Pero, lo que más llama la atención es la belleza con que representaba las relaciones matemáticas. ¡Era un amante de los números!. Suyas son:

En 1912 fue animado a comunicar sus resultados a tres distinguidos matemáticos. Dos de ellos no le respondieron, pero sí lo hizo Godfrey Harold Hardy, de Cambridge. Hardy estuvo a punto de tirar la carta, pero la misma noche que la recibió se sentó con su amigo John Edensor Littlewood, a intentar descifrar los 120 teoremas que acompañaban la misiva. Terminaría diciendo: "Esta es la obra de un genio". Invitado por Hardy, Ramanujan partió para Inglaterra en 1914 y comenzaron a trabajar juntos. En 1917 Ramanujan fue admitido en la Royal Society de Londres y en el Trinity College, siendo el primer indio que lograba tal honor. De salud muy débil, moría tres años después, cuando estaba como diríamos nosotros "en su salsa".

Para terminar:

La emocionante y humilde carta escrita a Hardy:
"Apreciado señor:
Me permito presentarme a usted como un oficinista del departamento de cuentas del Port Trust Office de Madrás con un salario de 20 libras anuales solamente. Tengo cerca de 23 años de edad. No he recibido educación universitaria, pero he seguido los cursos de la escuela ordinaria. Una vez dejada la escuela he empleado el tiempo libre de que disponía para trabajar en matemáticas. No he pasado por el proceso regular convencional que se sigue en un curso universitario, pero estoy siguiendo una trayectoria propia. He hecho un estudio detallado de las series divergentes en general y los resultados a que he llegado son calificados como "sorprendentes" por los matemáticos locales...
Yo querría pedirle que repasara los trabajos aquí incluidos. Si usted se convence de que hay alguna cosa de valor me gustaría publicar mis teoremas, ya que soy pobre. No he presentado los cálculos reales ni las expresiones que he adoptado, pero he indicado el proceso que sigo. Debido a mi poca experiencia tendría en gran estima cualquier consejo que usted me hiciera. Pido que me excuse por las molestias que ocasiono.
Quedo, apreciado señor, a su entera disposición .
S. Ramanujan."

Una de las anécdotas más famosas del genial Ramanujan:

La protagoniza con el propio G.H.Hardy. “Éste visitó a Ramanujan en el hospital, que se encontraba ya enfermo. Para darle conversación Hardy señala que el número del taxi que lo había traído, el 1729 era un número bastante soso, a lo que Ramanujan responde inmediatamente: ¡No, Hardy, No!. Se trata de un número muy interesante. Es el número menor que puede expresarse como suma de dos cubos dos maneras distintas”

Matemáticas y Cine

Cube

Cube cuando se estrenó en los cines pasó prácticamente inadvertida, pero el formato de video y el boca a boca la catapultó como uno de los clásicos del cine de ciencia ficción.

La película comienza y termina de forma extraña, dejando al espectador que razone y que saque sus propias conclusiones, el objetivo es que intente descubrir los motivos de la creación del cubo.

Sipnosis

Seis personas, desconocidas entre si, se despiertan una mañana en un espacio cerrado en forma de cubo. Entre esas personas están un escapista, un policía, una persona discapacitada, una medico, una brillante estudiante de matemáticas y una persona nihilista (de gran importancia en la trama)
El cubo está formado por compartimentos cúbicos que forman a su vez un cubo madre de grandes dimensiones. Estos habitáculos pueden ser de dos tipos: libres o con trampas, dependiendo del numero de serie que posea. Esas series de números tienen una relación lógica que tratan de resolver los ocupantes del cubo.
En Cube la ciencia juega un papel muy importante, en especial las matemáticas, conformando la trama de una forma exacta y sin rodeos.

Reparto
Nicole De Boer ( LeavenNicky), Guadagni (la doctora Hellen Holloway), David Hewlett ( David Worth), Andrew Miller (Kazan), Wayne Robson (Rennes), Maurice Dean Wint (Quentin).

Año

1997

La Ley de Titius-Bode

Distancia de los planetas al sol
La primera vez que escuché hablar de la ley de Titius-Bode me quedé impresionado al ver cómo las distancias de los planetas al sol encajaban prácticamente de forma perfecta con esta ley matemática. Es curioso este orden que gobierna la naturaleza. Veamos la apasionante historia llena de traiciones y de perseverancia que rodea la ley.

Johann Daniel Titius (1729-1796), profesor de matemáticas, al traducir libro del naturalista suizo Charles Bonnet, agregó un párrafo acerca de los planetas en el que mostraba que sus distancias al Sol se atienen a una fórmula cuando se miden en unidades astronómicas (una unidad astronómica [UA] es igual a la distancia media de la Tierra al Sol 147.597 x 10^6 km).
La fórmula opera de este modo: comenzando la serie de números por el 0, suma 3 y luego multiplica por 2 el resultado. Así se obtiene 0-3-6-12-24-48, etcétera. Suma 4 a cada uno de estos números obtenidos, y divide el resultado por 10 y se obteniendo la siguiente secuencia de números: 0,4 - 0,7 - 1,0 - 1,6 - 2,8 - 5,2 - 10,00 - 19,6 -38,8.

Serie original	Más 4	Dividido por 10
0	4	0,4
3	7	0,7
6	10	1,0
12	16	1,6
24	28	2,8
48	52	5,2
96	100	10,0
192	196	19,6
384	388	38,8

Es sorprendente que los siete primeros números de la tercera columna salvo el 2,8 describan con gran exactitud la distancia de los planetas al sol. Pero por desgracia el libro que traducía Titius junto con esta fórmula cayeron en el olvido.
La historia se retoma cuando Bode (astrónomo alemán) en 1772 escribe otro libro de introducción a la astronomía en el que incluye esta fórmula sin mencionar a su autor Titius (por lo que esta relación es conocida por muchos como la ley de Bode sólamente), y en el que pone de manifiesto su interés por descubrir qué pasa con el 2,8. ¿Habría otro planeta en esa zona que se desconocía?.

Nueve años después, otro famoso astrónomo William Herschel, descubre Urano a 19,18 UA, ¡¡ sorprendente, La fórmula predecía 19,6!! Esto hizo pensar dos cosas, la fórmula era verdadera y algo tenía que haber en el 2,8. ¡¡ Sigamos buscando, por favor!!

Y así fue, tenía razón, algo pasaba y algo había. ¡Viva el romanticismo!, ¡las matemáticas se salían con la suya!. El 1 de enero de 1801 Giuseppe Piazzi descubrió Ceres, el primero y mayor de los asteroides que giran alrededor del Sol, a unas 2,77 UA, entre Marte y Júpiter, cerquísima de lo que establece la ley de Titius-Bode. En esa zona posteriormente los científicos encontraron el llamado cinturón de asteroides (Pequeños trozos de rocas, que según algunos científicos podrían provenir de algún planeta que existió en esa zona).

Los astrónomos utilizaron afanosamente la ley de Titius-Bode para localizar Neptuno, pero éste demostró ser una anomalía dentro del sistema, estando significativamente más cerca de lo esperado. Sin embargo, Plutón estaba a la distancia predicha cuando se descubrió en 1930.

Bertusex

Alberto en un día de trabajo en Inglaterra, un tío elegante.

La palabra Bertusex no está recogida en la R.A.E. pero a mi amigo Alberto le va como anillo al dedo, y sobre todo si luego la terminas con un seeeee, junto con un ligero vaivén de la cabeza.

Alberto Navarro Zamora, granadino de pura cepa como él se considera, ha estudiado Farmacia y Ciencia y Tecnología de los Alimentos en la Universidad de Granada. Actualmente se encuentra trabajando en Inglaterra en una farmacia de la famosa ciudad de Oxford.

Pero Alberto destaca aparte de lo anterior, por su arte a la hora de contar su historias, por su sentido del humor con su famoso chiste del barón rojo, por el éxito con las chicas, por sus mangas cortas en invierno acostumbrado que está él de su etapa de leñador en Barmouth, por sus interminables horas de jugar al tenis con su gran y fuerte amigo Sam, por encantarle la naturaleza y en especial las tortugas, por su brazo bien formado y que por lo le gusta enseñarlo, por sus piques con Jose en el baloncesto, por su inglés con esos "whatever you want" tan característicos suyos, por sus pájaras, por ver conejos blancos cuando nadie los ve, por las lunas llenas, por su número mágico "el 20", por su casa del pozuelo de la que siempre habla y rara vez nos invita (y cuando lo hace se lía el taco) y por un montón de cosas más, pero sobre todo por lo buen amigo de sus amigos que es. Desde Spain, tus amigos te mandamos un saludo y un fuerte abrazo.

Aquí os presento "algunas fotos" de nuestro ilustre compañero:

Demostrando su equilibrio

Romántica pareja con los típicos trajes canarios

Curiosidades Numéricas

Algunas personas suelen decir, ¿Para qué sirven las matemáticas?. Las matemáticas están en todo lo que nos rodea, lo que pasa que hay que mirar con los ojos adecuados.
Por ejemplo, nosotros en nuestro día a día estamos rodeados de números, y muchos de ellos bastante grandes o muy pequeños, veamos algunos ejemplos:

• Los latidos del corazón que nos quedan:
  "Sabiendo que el corazón humano late a razón de 72 latidos por minuto, si la media de vida del ser humano está en unos 74 años, nuestro corazón latirá la cifra de 2.800.396.800 veces"
• Número de pelos en las cabezas de todo el mundo:
  "Según los cálculos de un aficionado, si se estima que cada persona tiene 125.000 pelos (algunos menos) y hay unos 6.000.000.000 de personas en la tierra, el resultado es: 750.000.000.000.000"
• Una multiplicación curiosa:
  Algunas veces las matemáticas te sorprenden con cosas cómo estas, dos números en principio tan dispares cumplen que su producto da un número que es lo de más exacto.
  8.589.934.592 x 116.415.321.826.934.814.453.125 = 1.000.000.000.000.000.000.000.000.000.000.000
• Número de cigarrillos que se fuman al día:
  Cada año se fuman en Estados Unidos 500.000.000.000 cigarrillos
• ¿Cuánto crece el cabello humano?:
  El cabello humano crece a razón de 0'000000016 kilómetros por hora
• El volumen total de la sangre humana existente en el mundo:
  Si de los seis mil millones de habitantes de la tierra se supone que cada uno contiene de promedio 4 litros de sangre se llega a que existen 24000000000 de litros de sangre circulando por las venas y arterias de toda la humanidad
• El número de estrellas en nuestra galaxia:
  Se estima que existen 200000000000 estrellas
• El número de granos de arena en el desierto del Sáhara:
  Se estima su número en 16.000.000.000.000.000.000.000
  
  Fuente: La sonrisa de Pitágoras

Los Montes de Anaga

Cuando uno piensa en Tenerife se te vienen a la cabeza las playas, el sol, las discotecas y sus papas arrugás. Pero esta isla es mucho más, uno de los sitios que más me ha gustado conocer han sido los montes de Anaga.

Esta zona situada cerca de la localidad de la Laguna permite adentrarte en pueblecitos pequeños (Taganana, El Batán, Chinamada...) dónde el tiempo parece no haber pasado por ellos, te permite ver lo dura que ha tenido que ser la vida para las gentes que los habitaban (algunos de ellos no han tenido luz hasta hace relativamente poco) y lo inteligentes que han sido para adaptarse a esas condiciones e incluso sacar provecho de ellas (cultivos en terrazas, cuevas).

También, Anaga destaca por sus preciosos paisajes con ese azul del océano de fondo, esa vegetación a veces exuberante que llama la atención en algunas zonas porque no olvidemos que estamos en una isla volcánica, y esas curiosas plantas que te encuentras mientras caminas y que los lugareños han utilizado a veces con motivos medicinales.

Y lo mejor de todo, que existen un montón de senderos que te permiten disfrutar de Anaga caminando (Es habitual sobre todo ver a alemanes e ingleses andurreando por allí). Algunos de los senderos terminan cerca de alguna playa, por lo que después de una larga caminata un bañito es la mejor medicina para recuperarte.

• Para más información: Punto de Información de la Cruz del Carmen, la Oficina de Información Parque Rural 922 633 576 y en el siguiente enlace http://www.puntoinfo.idecnet.com/index.php?lang=1
  Y desde aquí gracias a Israel y a Carmen por esas preciosas excursiones por el parque.

El PageRank

PageRank. El algoritmo que cambió Internet.
En 1998, dos jóvenes estudiantes de informática de la universidad de Stanford (Lawrence Page y Sergey Brin) proponen en su proyecto de investigación un sencillo algoritmo llamado PageRank que ordenaba un listado de páginas según su relevancia. Este algoritmo sería la base de un nuevo buscador "Google" (ahora la preferencia de millones de internautas), que en pocos años desplazaría a los buscadores ya existentes como Yahoo o Altavista.

El PageRank (PR) es un valor numérico que representa la importancia o relevancia que una página web tiene en Internet. Google se hace la idea de que cuando una página coloca un enlace (link) a otra, es de hecho un voto para esta última.
Cuantos más votos tenga una página, será considerada más importante por Google. Además, la importancia de la página que emite su voto también determina el peso de este voto. De esta manera, Google calcula la importancia de una página gracias a todos los votos que reciba, teniendo en cuenta también la importancia de la página que emite el voto. Una página que está enlazada por muchas páginas con un PageRank alto consigue también un PageRank alto.

El PageRank de la barra de Google va de 0 a 10. Diez es el máximo PageRank posible y son muy pocos los sitios que gozan de esta calificación, 1 es la calificación mínima que recibe un sitio normal, y cero significa que el sitio ha sido penalizado o aún no ha recibido una calificación de PageRank.

Sophie Germain

Marie-Sophie Germain (1 de abril de 1776 – 27 de junio de 1831), se crió en unos años donde las revueltas políticas y los cambios sociales en Francia crearán en ella la certeza de que la ciencia y en especial las matemáticas iban a ser sus vias de escape hacia una cierta estabilidad.
Sophie fue practicamente una matemática autodidacta que ha pasado a la historia porque hizo importantes contribuciones a la teoría de números (participó en la demostración del último teorema de Fermat, y tiene en su honor un tipo de números primos) y la teoría de la elasticidad.

La historia de Sophie es la de una matemática brillante que no pudo lograr su pleno desarrollo porque en sus años de formación no pudo acceder a una educación matemática formal (sus padres no querían que se dedicara a las matemáticas, y en general estaba mal visto e incluso no estaba permitido). También en su madurez también se vio obligada en determinadas ocasiones a trabajar en solitario, o incluso se tuvo que hacer pasar por un hombre para ser escuchada, porque una jerarquía científica totalmente masculina, la excluía de toda posibilidad de entrar en un mundo sólo de hombres.

Muy interesante es la historia con el famoso matemático Carl Fiedrich Gauss.

Gauss estaba totalmente sorprendido por los artículos enviados en sucesivas cartas por un tal señor "Le Blanc", (el pseudónimo usado por Sophie) así que le pide una entrevista personal. Así Sophie se ve obligada a desvelar su identidad en una carta a Gauss. Y éste, uno de los mejores matemáticos de la historia y, le responde con estas admirables palabras: "Pero cómo describirte mi admiración y asombro al ver que mi estimado corresponsal Sr. Le Blanc se metamorfosea en este personaje ilustre que me ofrece un ejemplo tan brillante de lo que sería difícil de creer. La afinidad por las ciencias abstractas en general y sobre todo por los misterios de los números es demasiado rara: lo que no me asombra ya que los encantos de esta ciencia sublime sólo se revelan a aquellos que tienen el valor de profundizar en ella. Pero cuando una persona del sexo que, según nuestras costumbres y prejuicios, debe encontrar muchísimas más dificultades que los hombres para familiarizarse con estos espinosos estudios, y sin embargo tiene éxito al sortear los obstáculos y penetrar en las zonas más oscuras de ellos, entonces sin duda esa persona debe tener el valor más noble, el talento más extraordinario y un genio superior. De verdad que nada podría probarme de forma tan meridiana y tan poco equívoca que los atractivos de esta ciencia que ha enriquecido mi vida con tantas alegrías no son quimeras que las predilección con la que tú has hecho honor a ella."

Paco de Jerez.

Paco campeón del Torneo de Ajedrez de Chipiona

Bajo este pseudónimo propio de un torero, o de un bailaor de flamenco, conocemos a Francisco Fernández Montero.

Paco nació en Jerez, y es casi matemático porque le faltan algunas asignaturas para terminar, pero está en ello, su principal afición es el ajedrez (da clases de ajedrez en diferentes colegios de Jerez) y actualmente es uno de los mejores jugadores andaluces del momento.

Paco destaca por su buen humor (siempre tiene un chiste preparado), por sus piques con Rafa "El niño de Loja" (sobre todo por cuestiones de amores, veremos lo que desencadena la siguiente foto, jejejeje), por lo desordenado que tenía el cuarto en Granada, y sobre todo por su generosidad y lo buena persona que es.

En esta foto lo vemos con una chica en Tenerife (Gádor, también matemática, rompiendo estereotipos). A Paco se le está callendo la baba y todos nos preguntamos. ¿Cómo la engañó para que se echara esta romántica foto con él? Nadie lo sabe, pero seguro que es la envidia de muchos, eh Rafa.

La Sucesión de Fibonacci

¿Serías capaz de continuar? 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ...

Se llama sucesión a una secuencia de números para los que se puede encontrar una regla que nos permite calcular todos los números de esa secuencia. La sucesión de Fibonacci fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII (conocido como Fibonacci), que aparte es famoso por su libro "Liber Abaci" dónde por primera vez usa las cifras hindúes y el cero (0,1,2...,9) mostrando en él numerosos ejemplos de su facilidad para el cálculo sobre el sistema de numeración (El Romano) que hasta antes se había usado.

Es una de las sucesiones más famosas de la historia porque tiene numerosas aplicaciones fundamentalmente en la naturaleza, aunque también aparecen aplicaciones en otros campos como la informática. Su relación como veremos posteriormente con el número de oro, hace que esté presente en todos aquellos procesos de la naturaleza dónde se produce un crecimiento proporcionado, es decir, que mantiene la forma. También ha aparecido en el libro y posterior película "El Código Da Vinci" , de hecho era una de las pistas que comenzaban la historia en el museo del Louvre de Paris.

La espiral que se forma en el crecimiento de algunos animales está relacionada con el número de oro, y a su vez con la sucesión de Fibonacci.

El origen de esta sucesión está relacionado con la reproducción de los conejos, Fibonacci plantea el siguiente acertijo: "Una pareja de conejos tarda un mes en alcanzar la edad fértil, a partir de ese momento cada vez engendra una pareja de conejos, que a su vez, tras ser fértiles engendrarán cada mes una pareja de conejos. ¿Cuántos conejos habrá al cabo de un determinado número de meses?."

Dibujando la situación en el gráfico anterior aparecen los términos de esta sucesión

Se llama filotaxia a la ciencia que estudia la disposición de las hojas en las ramas. Siempre las hojas tienden a buscar el máximo de luz por eso ninguna hoja nace justo en la vertical de la anterior, pues mira que coincidencia que la distribución de las hojas alrededor del tallo de las plantas se produce siguiendo la sucesión de Fibonacci.

El número de espirales en numerosas flores y frutos también se ajusta a parejas consecutivas de términos de esta sucesión: los girasoles tienen 55 espirales en un sentido y 89 en el otro, o bien 89 y 144. Las margaritas presentan las semillas en forma de 21 y 34 espirales. Y cualquier variedad de piña presenta siempre un número de espirales que coincide con dos términos de la sucesión de los conejos de Fibonacci, 8 y 13; o 5 y 8.

Una de las propiedades más interesantes de esta suceción es que si dividimos los términos consecutivos de la sucesión nos vamos acercando de forma progresiva al número de oro = 1.618033.... Veámoslo: 1/1 = 1, 2/1=1, 3/2=1.5, 5/3=1.66, 8/5=1.6, 13/8=1.625, 21/13=1.6153 y así sucesivamente.

Ricardo Sarrión, Jienense de pro.

Ricardo es otro matemático más de esa magnífica promoción del 93 que estudiamos en Granada. A él siempre le gustaron más los negocios y la informática que los niños y el mundo de la enseñanza.
Nacido en Jaén, gran cantante, deportista, y desde siempre muy aficionado al Real Jaén que esperemos pronto recupere la categoría que se merece con jugadores como los de antaño "Ése Rueda Oeeeé".

En esta foto demostrando su arte en la captura de la trucha burgalesa, jejeje.

Magnus Carlsen. Niño Prodigio

Foto de Henrik Larsen

Magnus (30/11/1990), es una de las estrellas actuales del ajedrez. Este joven jugador comenzó a los 5 años a jugar al ajedrez, a los 9 le ganaba a su padre y en el año 2004 (con 13 años, 4 meses y 27 días) se convierte en el gran maestro más joven de la historia del ajedrez. Actualmente es el tercero más joven detrás Sergey Karjakin y Parimarjan Negi.

Carlsen destaca por su gran memoria fotográfica (a los 5 años conocía todas las capitales del mundo), odia las matemáticas (rompiendo tópicos), su asignatura preferida es el inglés y la geografía, y como a la mayoría de los chavales le encanta el fútbol y las consolas.

Magnus Carlsen con 13 años

Uno de sus mejores resultados a nivel mundial lo obtiene en marzo de 2007, en el Torneo Internacional de Ajedrez Morelia-Linares (uno de los más importantes del mundo, antes llamado sólamente Linares). Allí Carlsen quedó clasificado el 2º, con 7.5 puntos en 14 partidas, tras Anand.
En el ranking de la FIDE de Julio del 2007 esta dentro de los 20 mejores jugadores del mundo, situado en el puesto 17, con 2710 puntos ELO.

Mancala

Historia del juego.
Bajo el nombre de Mancala quedan englobados una serie de juegos de tablero de características similares. Este tipo de juegos se piensa que tuvo se origen en África y en el antiguo Egipto, de hecho se han encontrado tableros tallados en Menfis, Tebas y Luxor.(No obstante, el tablero más antiguo conservado de terracota encontrado en la isla de Creta data del siglo XVIII a.C.). En el siglo XIX los viajeros europeos eran retados a jugar mancala en los cafés de El Cairo, y por costumbre el perdedor pagaba los cafés tomados durante el juego. Los esclavos africanos lo llevaron consigo al continente americano (el juego se popularizó principalmente en el Caribe y en la costa este de Sudamérica). Los juegos de mancala han constituido desde siempre el entretimiento del pueblo y están presentes en todos los estratos sociales. Actualmente se conocen muchas variantes de este juego con nombres como wari, awale, adi, ti, walu, entre otros, y se juega en todo el mundo.

Aplicaciones de este juego en clase.
Estos juegos permiten que los alumnos/as pueden desarrollar habilidades sociales con la práctica de este juego y desde el punto de vista de las matemáticas permite que el alumno tenga que elaborar estrategias para ganar, anticiparse a las jugadas pensando lo que puede hacer el contrincante y por supuesto saber contar. Todas estas características son fundamentales en el pensamiento matemático.

Posición inicial del Awalé

Cómo se juega (explicación rápida).

El juego más difundido de Mancala es el Awalé. En él aparecen 2 hileras de 6 hoyos que tienen las llamadas "semillas" (4 por cada hoyo), más dos hoyos más grandes destinados a depositar las piezas capturadas. El Awalé lo juegan 2 jugadores, cada uno se dispone a cada lado del tablero y controla los 6 hoyos de su lado. Las dos operaciones básicas del juego son sembrar y recolectar:

1. Siembra: Cuando un jugador tiene que mover elige un hoyo que no esté vacío, y siembra(distribuye) todas las semillas que contiene, una por hoyo, en hoyos correlativos al de partida en sentido contrario al de las agujas del reloj. Nota: Si al sembrar, en el hoyo elegido hay suficiente semillas como para dar la vuelta completa al tablero al llegar al hoyo de partida lo saltamos y seguimos con el hoyo siguiente. Y si nos toca sembrar y el adversario no tiene semillas en su campo debemos procurar que le llegue una semilla al menos.
2. Recolección:Al finalizar la siembra, podemos recoger las semillas de los hoyos rivales con dos o tres semillas que las hemos ganado. Nota: Un jugador no puede realizar una siembra que deje al adversario sin semillas.

La partida termina cuando:

1. Un jugador no tiene semillas en su campo y el otro, al que le toca jugar no puede darle ninguna por medio de alguna jugada legal.
2. Quedan pocas semillas y se entra en un círculo vicioso.
3. Un jugador abandona porque el contrario ha conseguido capturar más de 24 semillas.

Isla Cristina. Un Mar de Luz

El origen de Isla Cristina (o Isla, como se la conoce entre sus gentes) es muy reciente, se remonta a la segunda mitad del siglo XVIII tras el terremoto de Lisboa (el año pasado se cumplieron 250 años de su fundación). En esa época pescadores provenientes del Mediterráneo, catalanes y levantinos fundamentalmente, establecieron aquí sus bases de pesca. Dedicados sobre todo a la sardina y al atún, construyeron un poblado que debido a la enorme riqueza de estos caladeros fue creciendo espectacularmente.
El primer nombre de la población fue el de "La Higuerita", en honor al árbol simbólico junto al que se estableció un pozo de agua dulce y los primeros chamizos. Hacia el 1834 se modificaría su nombre por el actual, Isla Cristina, como agradecimiento a la reina María Cristina por la ayuda humanitaria prestada en una epidemia de cólera.

Situada en el litoral occidental de la provincia onubense y en el suroeste de la región andaluza, está enclavada en un emplazamiento privilegiado, cuenta con doce kilómetros de playas de blanca y fina arena, transparentes aguas y un montón de horas de sol.

Sus gentes, sus tradiciones, su carnaval (uno de los más famosos de Andalucía), su carácter marinero, sus expresiones, su olor a mar, su gastronomía, la convierten en una población peculiar, diferente y con mucho encanto.
Para visitar: "El Parque Natural de las Marismas de Isla Cristina", las puestas de sol junto al faro.
Para comer: Pescado en general, pero recomiendo coquinas, sardinas y el atún (preparado de mil formas).

Para más información:

• Web del ayuntamiento de Isla: http://www.islacristina.org/
• Web interesante de la provincia: http://www.playasdehuelva.org/
• Aquí puedes escuchar la higuerita marinera (Himno de Isla) en las comparsas del año 1982: http://www.carnavaldeislacristina.com/

El cubo de Rubik

Mis tíos y primos en el Cubo de Rubik
El cubo de Rubik es un rompecabezas mecánico inventado por el escultor y profesor de arquitectura húngaro Ernö Rubik en 1974.

Existe todo un mundo alrededor de este aparente inocente juego.
Se pueden encontrar campeonatos a nivel nacional y a nivel mundial en los que personas tratan de resolverlo bajo el agua, con una sóla mano, con los ojos vendados, y por supuesto con dos manos.


En estos concursos también es frecuente ver pruebas de rapidez en armar el cubo (creo que el record está en 11.13 segundos establecido por un estudiante americano de 20 años el pasado año).
También no sólo está el clásico cubo de rubik, existen otros modelos de diversas formas (4x4, esférico, octogonal, y muchos más).

Desde el punto de vista de la didáctica el cubo de rubik es una excelente herramienta para usarla en clase con los alumnos para trabajar diversos aspectos del curriculum. Pero mucho más, desde siempre ha interesado a los matemáticos y a los aficionados a las ciencias, de hecho hay algunas personas que por ejemplo investigan el mínimo número de movimientos posible para armar el cubo (el llamado número de Dios), el pasado 17 de agosto se publicó en el país que investigadores estadonidenses habían hallado que este número era 26, pero se cree que puede ser menor de 20.
Para finalizar, aquí encontrais varios enlaces para saber más del cubo de rubik (la forma de resolverlo, curiosidades, campeonatos, etc)

• http://www.rubikaz.com/
• http://es.wikipedia.org/wiki/Cubo_de_Rubik
• http://www.elpais.com/articulo/internet/cubo/Rubik/resuelto/26/movimientos/elpeputec/20070817elpepunet_2/Tes
• http://www.speedcubing.com/chris/

Y un enlace a diferentes vídeos sobre el cubo de rubik en la página de youtube.com (algunos alucinantes, como el de la niña china que arma el cubo en 114 segundos)

• http://www.youtube.com/results?search_query=cubo+de+rubik

Fotos Curiosas

No se lo que pasa, pero cuando me pongo a ver fotos de los viajes que hemos hecho, siempre aparecen fotos que no recuerdo haberlas hecho, y sin embargo luego son unas de las que más me gustan.

Esta foto la he titulado "Desfile Militar". En ella podemos ver cómo mis amigos pasean de forma ordenada por cualquier sendero. Recuerda a cualquier portada de un disco de Duncan Dhu.

Esta segunda foto la he titulado "Alumno despitado", personalmente me recuerda a una clase en la que siempre hay algún alumno travieso que está por los cerros de Úbeda mientras los otros alumnos siguen atentos la explicación del profesor.

En la tercera y última foto, que he titulado "Viva la alcaldesa" me recuerda al mitin después de ganar las elecciones que todo partido político (con todos sus componentes) realiza en pos de celebrar con sus votantes el triunfo electoral. En esta foto es de destacar al concejal de trabajo (el hombre rubio grande y fuerte a la izquierda de la alcaldesa) que ha empezado aburrio su mandato.

La letra del DNI

Una de las aplicaciones a la vida real más básicas de la división de números naturales es el cálculo de la letra del DNI.
Tan sólo necesitamos dividir el número de nuestro DNI entre 23. El resto de la división va a ser siempre un número (si no nos equivocamos en las cuentas, jejeje) comprendido entre 0 y 22. Por lo que para conseguir la letra miramos en la siguiente tabla el número conseguido y la obtenemos.

Resto	Letra	Resto	Letra
0	T	12	N
1	R	13	J
2	W	14	Z
3	A	15	S
4	G	16	Q
5	M	17	V
6	Y	18	H
7	F	19	L
8	P	20	C
9	D	21	K
10	X	22	E
11	B

El código de barras

Cada vez que queremos comprar un producto ahí aparece el código de barras, esos númeritos con esas barras negras y blancas. Las empresas usan los códigos de barras para llevar el control del número de productos que tienen almacenados y para agilizar el proceso de cobro fundamentalmente.

Pero, ¿Qué son esas barras?

El sistema empleado para convertir un código de barras en una información útil consiste en iluminarlo con una luz visible e infrarroja, que es reflejada de nuevo hacia el aparato lector. Esta información se convierte en impulsos eléctricos que, mediante un algoritmo matemático, se traducen en un código binario, con el que un ordenador puede trabajar. El número 1 se representa por una barra negra y el número 0 por una barra blanca (o espacio en blanco). La forma de asignar ceros y unos viene determinada por convenios internacionales, no obstante existen elementos fijos como las barras largas del principio y del final (código 101) y las barras centrales (código 01010).

Y, ¿qué son esos números?

En Europa se utiliza el EAN (European Article Numbering). Se trata de un estandar internacional de 13 dígitos, creado en Europa en 1977, que en la actualidad opera en más de 80 países y es compatible con el sistema Universal Product Code (UPC), utilizado en América del Norte y Canadá.

Los dos primeros dígitos se refieren al país, luego vienen dos grupos de 5 dígitos. El primer grupo de 5 dígitos se refieren a cada empresa, y el segundo grupo de 5 dígitos se refieren al producto.
El último dígito se llama de control, y se calcula mediante una fórmula matemática, que se resume de la siguiente manera:

• Sumamos las cifras de posiciones impares: (En el ejemplo: 9+0+1+0+2+0=12)
• Sumamos las cifras de posiciones pares, y el resultado se multiplica por 3:(En el ejemplo:9+0+0+7+6+1=23 ->3·23=69)
• Sumamos las dos cantidades obtenidas, y nos quedamos con la cifras de las unidades: (12 + 69 = 81 ->1)
• Restamos 10 menos la cifra obtenida y nos quedamos con la cifra de la unidades: (10 - 1 = 9) -> Dígito de control es 9 !!!!!!

Nota: El código del pais no quiere decir que el producto haya sido fabricado en ese país, dado que el responsable de la comercialización utiliza el código que le ha sido asignado en el país en el que se pone a la venta. Por ejemplo, un rico jamón de jabugo puede llevar el código de Italia.

La Catenaria

Casa Batlló (A. Gaúdí)

Estamos acostumbrados a ver curvas en nuestro día a día. Muchas de ellas nos las brinda la naturaleza, pero otras, como el trazado de carreteras, vías ferroviarias o las escaleras de caracol han requerido el desarrollo de una sofisticada geometría y unos conocimientos de cálculo importantes.

Una de esas curvas que forman parte de nuestro día a día, es la catenaria. La catenaria es la curva que describe una cadena suspendida por sus extremos y que se encuentra sometida a un campo gravitatorio uniforme, o dicho de otra manera, es la curva que forman los cables o los collares de perlas cuando se dejan caer libremente sujetos por ambos extremos.

Durante siglos, los matemáticos intentaron determinar de qué curva se trataba. Creían que era una parábola, ya que era a lo que más se parecía, pero no fue hasta principios del siglo XVIII cuando los hermanos Bernouilli (famosa familia de matemáticos), gracias a sus conocimiento de física determinaron su ecuación.

(h es un parámetro que controla la apertura de la curva)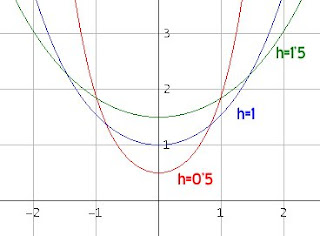

El uso de la catenaria en la vida real es evidente, las guirnaldas que adornan muchas fiestas, los cables de alta tensión, algunos puentes son catenarias.
Así mismo, en arquitectura, la curva catenaria invertida es el trazado perfecto para un arco (dado que toda la línea de presiones sigue la forma de la curva), además de tener una importante componente estética debido a la sutileza de su perfil. Esta tipo de curva fue empleada por el genial arquitecto Antoni Gaudí como arco de sustentación en muchas de sus obras (Colonia Güell, Casa Batllo, la Pedrera y en muchas más).